纵观各大系统考试真题，不定方程都考的都比较简单，且变型少，技巧性比较强，当掌握其解题方法后，不定方程只要考到就是送分，重要的话说三遍，不定方程考到就是送分，考到就是送分，送分……

常见考察形式为：

①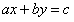（其中）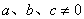

②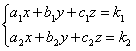（不定方程组）

解不定方程的方法：代入排除法，具体如下：

①直接代入法：直接要求的是或者

例：,其中x、y都是正整数，求y=（   ）。

A.2      B.3     C.4       D.5

【答案】A

【解析】要求的是y的值，A、B、C、D中一定有一个是正确答案，所以只需要一个个带入验证即可，只需要保证求出来的x也是正整数就可以，带入A选项，当y=2时，x=4，满足条件，继续验证后面的选项都不满足，所以A当选。

②奇偶性：当x、y的系数为一奇一偶时，可以使用奇偶性解不定方程。

例:,其中x、y都是正整数，求x=（   ）。

A.3      B.4     C.5       D.6

【答案】C

【解析】6y为偶数，41为奇数，由奇偶性运算可得7x为奇数，则x也是奇数，故可以排除B、D选项，剩下A、C，带入A选项，当x=3时，21+6y=41，此时y不是整数，排除，答案选C。

③倍数特性：当x、y的系数与右边常数存在倍数关系时，可以使用倍数特性解不定方程。

例: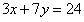，其中x、y都是正整数，求x=（   ）。

A.1      B.2     C.3       D.4

【答案】A

【解析】3x和24都是3的倍数，所以7y也是3的倍数，又y是整数，所以y是3的倍数，满足3的倍数有3、6、9……，但必须得保证x是正整数，所以只有当y=3时，x=1，符合条件，答案选A。

④尾数法：当x或y的系数为5的倍数时，可以使用尾数法解不定方程(一般会结合奇偶性)。

例: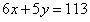，其中x、y都是正整数，求x-y=(    )。

A.3      B.4     C.5       D.6

【答案】D

【解析】其中6x和113分别是偶数和奇数，所以5y这个整体也是奇数，两个数的乘积是奇数，进一步得到y也是奇数，一个奇数与5相乘，它的尾数为5，所以6x的尾数为8,6与3或8相乘的尾数为8,故得到x的尾数为3或8，满足x的数有3、8、13、18……，当x=3时，y=19，x＜y，不符；当x=8时，y=13，同理不符；当x=13时，y=7，此时x-y=6，故答案选D。

⑤赋值法：大多数情况为不定方程组中含有3个未知数x、y、z，且求的是含有“x+y+z”的整体时，一般的操作为令x、y、z中的一项为0。

例:已知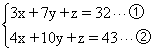，求x+y+z=(    )。

A.12 B.11 C.10 D.9

【答案】C

【解析】令y=0,则相当于将y消去了，则方程变为了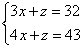，两式相减解得x=11,z=-1,根据题意可知要求的是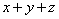的值，故。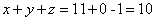

赋值法的特征为不会影响结果，也可以令x或z为0,最终“x+y+z”的结果始终不变，当然这里最简单的处理方式就是令y=0,后续的计算比较简单。

一般地像这一类型的题，还可以采取用配系数法，即令①×3-②×2结果刚好等于x+y+z=32×3-43×2=10，但这一方法要求对数字明感性比较强。